Apakah itu Voltan RMS ?8 min read
Terdapat dua jenis arus elektrik yang wujud, iaitu arus terus (DC) dan juga arus ulang alik (AC). Perbezaan dua jenis arus ini adalah arus DC mempunyai magnitud, atau nilai voltan yang tidak berubah manakala arus AC mempunyai nilai voltan yang sentiasa berubah. Perubahan voltan arus AC ini berubah dalam bentuk sinusoidal dalam satu kitaran. Contohnya, jika arus AC mempunyai voltan puncak bernilai 5V, arus AC akan mempunyai nilai yang berubah dari 5V hingga ka -5V dalam satu kitaran.
Dalam sistem arus elektrik DC, voltan dan arus adalah tidak berubah. Oleh itu tidak ada masalah untuk kita menyatakan nilai voltan arus DC. Contohnya arus DC yang mempunyai nilai voltan sebanyak 5V, kita akan menyatakan voltan arus DC tersebut adalam 5V. Namun, ianya tidak semudah itu bagi arus AC, kerana arus AC sentiasa berubah. Apakah nilai magnitud yang kita nak nyatakan pada arus AC yang berubah dari 5V ke -5V? Ya, kita boleh nyatakan nilai arus AC tersebut sebagai arus yang sentiasa mempunyai voltan puncak 5V, atau dengan ringkas 5Vpeak . Namun, hanya menggunakan voltan puncak tidak memberi representasi yang tepat kesan voltan AC terhadap litar elektrik. Walaupun voltan puncak menunjukkan nilai voltan maksimum dan minimum yang dicapai arus AC, namun ia tidak mengambil kita purata kuasa yang dihantar oleh arus AC dalam satu masa.
Oleh itu, untuk merepresentasikan kuasa yang arus AC hasilkan, lahirnya konsep voltan RMS. Mari kita lihat bagaimana voltan RMS didefinisikan.
Definisi Voltan RMS
Dalam pengenalan dia atas, kita telah bincangkan peranan voltan RMS dalam kuasa. Kuasa adalah tenaga yang dikeluarkan dalam satu jangka masa. Definisi bagi voltan RMS adalah “nilai voltan AC yang meberikan kesan pemanasan yang setara dengan voltan DC“. Kesan pemanasan disini adalah untuk merujuk kuasa yang dihasilkan oleh voltan RMS tersebut. Contohnya, palam kediaman keluarkan 240V AC, Ianya dalam unit Voltan RMS. Ini bermaksud, arus elektrik AC yang keluar dari palam kediaman kita memberikan kesan pemanasan sama seperti arus DC 240 V.
Singakatan pada RMS adalah “Root Mean Square”, atau dalam bahasa kita ialah punca min kuasa dua. Dalam erti kata lain, nilai punca kuasa dua bagi purata kuasa dua sesuatu kuantiti yang berubah dalam tempoh tertentu. RMS merupakan purata kuadratik. Ianya lebih kurang sama dengan purata yang biasa kita guna iaitu purata aritmetik dimana kita tambahkan kesemua nilai dan bahagikan dengan bilangan. Dalam purata kuadratik, kita tambahkan nilai yang dikuasa dua, bahagikan dengan bilangan dan akhir sekali mengira punca kuasa dua.
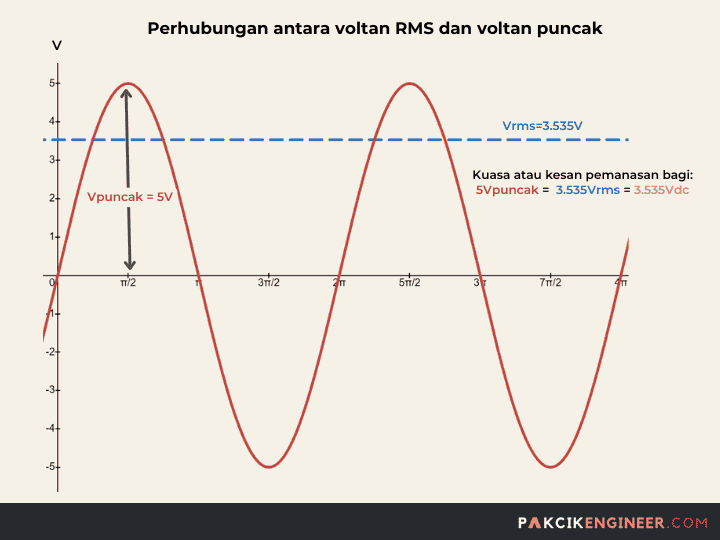
Perhubungan antara voltan RMS dan voltan puncak adalah seperti berikut:
V_{RMS}=\frac{V_{peak}}{\sqrt{2}}\\
V_{RMS}=0.707V_{peak}Ini bermakna, jika anda tahu voltan puncak sesuatu arus AC, anda boleh menentukan nilai Voltan RMS menggunakan formula tersebut. Sebagai contoh, jika voltan puncak arus AC adalah 5Vpeak , maka Voltan puncak adalah 0.707 X 5Vpeak = 3.535VRMS. Ini bermaksud, arus AC tersebut memberikan kesan pemanasan sama seperti arus DC 3.535V.
Cara menentukan voltan RMS
Cara grafikal
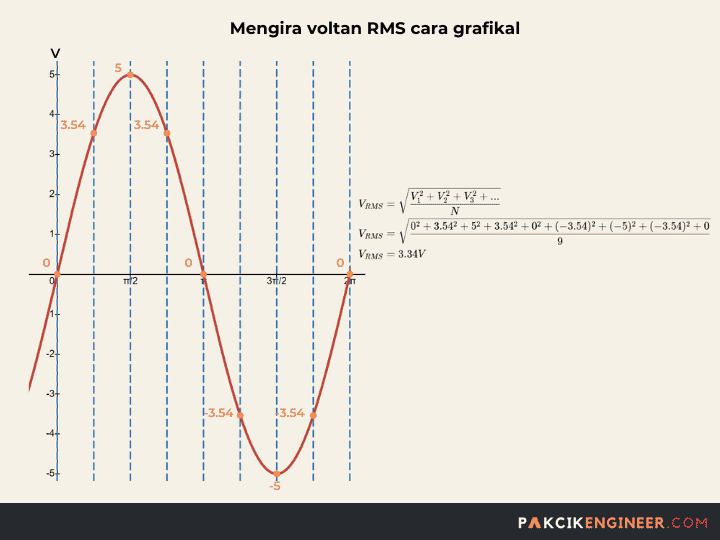
Untuk mengira voltan RMS menggunakan cara grafikal, kita lukiskan bentuk isyarat elektrik tersebut dan pecahkan kepada beberapa bahagian dengan sama rata. Lebih banyak bahagian kita pecahkan, lebih tepat pengiraan yang kita akan dapat. Kaedah ini juga dipanggil ‘mid-ordinate method‘. Berikut langkah pengiraan:
1. Pecahkan kepada bahagian yang sama rata.
2. Ambil nilai voltan semasa pada paksi y, pada setiap bahagian dipecahkan.
3. Kira kuasa dua bagi setiap nilai voltan semasa tersebut, dan tambahkan kesemunya.
4. Bahagikan dengan bilangan pecahan,
5. Kira punca kuasa dua.
Formula dan gambarajah dibawah menunjukkan cara pengiraan dengan lebih jelas. Contoh pengiraan dibawah menunjukkan nilai yang kita dapat adalah 3.34VRMS. Nilai ini dekat sekali dengan nilai sebenar yang kita harus dapat, iaitu 3.535VRMS. Ini kerana, untuk dapatkan nilai yang lebih tepat, kita perlu pecahkan dengan lebih kecil lagi.
Cara ini sesuai untuk pelbagai jenis bentuk isyarat elektrik, seperti isyarat sinusoid, segi tiga, segi empat dan sebagainya.
V_{RMS}= \sqrt{\frac {V_{1}^2 + V_{2}^2 + V_{3}^2 + ...}{N}}
\begin{equation}
\begin{split}
V_{RMS}&= \sqrt{\frac {V_{1}^2 + V_{2}^2 + V_{3}^2 + ...}{N}} \\
V_{RMS}&= \sqrt{\frac {0^2 + 3.54^2 + 5^2 + 3.54^2 +0^2 +(-3.54)^2 + (-5)^2+(-3.54)^2+0}{9}}\\
V_{RMS}&=3.34V
\end{split}
\end{equation}
Jika kita gunakan formula ringkas yang menghubungkan voltan puncak dan voltan RMS, kita akan dapat nilai yang sama. Mari kita lihat bagaimana perhubungan antara voltan RMS dan voltan puncak terhasil.
\begin{equation}
\begin{split}
V_{RMS}&=0.707V_{peak}\\
&=0.707 \times 5 \\
&=3.535V
\end{split}
\end{equation}Cara menerbitkan persamaan cara grafikal
Bagaimana persamaan diatas yang tadi diterbitkan? Untuk menghasilkan persamaan tersebut, mari kita berbalik kepada definisi voltan RMS, iaitu nilai voltan AC yang meberikan kesan pemanasan yang setara dengan voltan DC. Pemanasan mengeluarkan haba, dan haba ini merupakan satu bentuk kuasa. Kuasa yang dikeluarkan keatas perintang disebabkan voltan adalah P=V2/R . Kuasa yang dikeluarkan oleh arus DC adalah seperti berikut.
\begin{equation}
\begin{split} P_{DC}=\frac{V_{DC}^2}{R}\\
\end{split}
\end{equation}
Katakan terdapat satu arus AC, yang mempunyai voltan puncak Vp. Seperti yang kita tahu, voltan AC berubah dalam kitaran. Untuk kita tahu apakah kuasa yang dikeluarkan oleh arus AC, kita kena ambil beberapa bilangan sampel voltan AC dengan jarak sama diantaranya dan kira puratanya. Kaedah ini adalah dipanggil kaedah bergrafan atau juga dipanggil mid-ordinat.
\begin{equation}
\begin{split}
P_{AC} &=\frac{P_1 + P_2 + P_3 + ....}{N} \\
P_{AC} &=\frac{\frac{V_{1}^2}{R} + \frac{V_{2}^2}{R} + \frac{V_{3}^2}{R} + ....}{N}\\
&=\frac{V_{1}^2 + V_{2}^2 + V_{3}^2 + ...}{NR}
\end{split}
\end{equation}
Dimana N= bilangan sampel
Untuk menjawab persoalan apakah nilai setara voltan DC yang menghasilkan kesan pemanasan yang sama di dalam voltan AC, kita samakan persamaan (1) dan (2). Dengan menyusun semula persamaan tersebut, dan mencari nilai VDC , kita akan memperoleh nilai VDC . Nilai yang kita dapat ini adalah nilai voltan DC yang setara jika arus yang mengalir adalah arus DC. Jika kita lihat formula yang terhasil ianya merupakan punca purata kuasa dua yang kita bincangkan di awal topik. Oleh itu kita panggil nilai voltan ini adalah voltan RMS.
\begin{equation}
\begin{split}
P_{DC}&=P_{AC} \\
\frac{V_{DC}^2}{R} &= \frac{V_{1}^2 + V_{2}^2 + V_{3}^2 + ...}{NR} \\
V_{DC}^2&= \frac {V_{1}^2 + V_{2}^2 + V_{3}^2 + ...}{N} \\
V_{DC}&= \sqrt{\frac {V_{1}^2 + V_{2}^2 + V_{3}^2 + ...}{N}} = V_{RMS}
\end{split}
\end{equation}
Cara analitikal
Untuk mengaitkan voltan RMS dan voltan puncak, teori yang lebih kurang sama kita boleh pakai iaitu menyamakan kuasa yang dihasilkan oleh arus AC dengan arus DC untuk mencari nilai voltan DC yang setara. Namun kali ini, kita gunakan cara matematik untuk menganalisa arus AC. Berbeza dengan cara sebelum ini dimana kita mengambil sampel beberapa voltan di dalam graf, kali ini kita akan ungkapkan arus AC sinusoidal seperti berikut.
V_{AC}(t)=V_p cos(wt)Kuasa yang dihasilkan arus AC tersebut adalah:
\begin{equation}
\begin{split}
P_{AC} &=\frac{[V_{AC}]^2}{R} \\
P_{AC} &=\frac{[V_p cos(wt)]^2}{R} \\
\end{split}
\end{equation}
\begin{equation}
\begin{split}
P_{AC} &=\frac{\frac{1}{T}\int_{0}^T[V_p cos(wt)]^2}{R} dt \\
P_{AC} &=\frac{\frac{1}{T}\int_{0}^T V_p^2 cos^2(wt)}{R} dt \\
P_{AC} &=\frac{V_p^2}{TR} \int_{0}^T cos^2(wt) dt \\
\end{split}
\end{equation}Masih berpegang kepada definisi voltan RMS, iaitu nilai voltan AC yang meberikan kesan pemanasan yang setara dengan voltan DC.
Kita Samakan kuasa yang dihasilkan oleh arus DC dengan arus AC, dengan menayamakan persamaan (2) dan (7):
\begin{equation}
\begin{split}
P_{DC} &=P_{AC}\\
\frac{V_{DC}^2}{R} &=\frac{V_p^2}{TR} \int_{0}^T cos^2(wt) dt \\
V_{DC}^2 &=\frac{V_p^2}{T} \int_{0}^T cos^2(wt) dt \\
\end{split}
\end{equation}Satu kitaran isyarat ulang alik AC mempunyai kala (period) T . Oleh itu, kita lakukan operasi pengamilan (integration) pada had 0 hingga T, dan seterusnya gantikan ω dengan 2π/T.
\begin{equation}
\begin{split}
V_{DC}^2 &=\frac{V_p^2}{2T} \left [ t+ \frac{1}{2\omega} \sin(2\omega t) \right ] ^T_0 \\
V_{DC}^2 &=\frac{V_p^2}{2T} \left\{ \left [ T + \frac{T}{2\pi}\sin(2(\frac{2\pi}{T})T \right ] - \left [ 0 + \frac{T}{2\pi}\sin(2(\frac{2\pi}{T})0 \right ] \right\} \\
V_{DC}^2 &=\frac{V_p^2}{2T} \left\{ \left [ T +0 \right ] - \left [ 0 +0 \right ] \right\} \\
V_{DC}^2 &=\frac{V_p^2}{2} \\
V_{DC} &=\sqrt{\frac{V_p^2}{2} } \\
V_{DC} &=\frac{V_p}{\sqrt{2}} =V_{RMS}\\
V_{RMS} &=0.707V_{p}
\end{split}
\end{equation}Dengan ini, kita telah berjaya meringkaskan perhubungan antara voltan puncak dan voltan RMS yang saya gunakan di awal artikel. Perlu diingat bahawa formula ini hanya boleh dingunakan untuk arus elektrik yang berbentuk sinusoid sahaja. Untuk bentuk arus elektrik yang lebih kompleks seperti arus segi empat dan segi tiga, anda perlu mula balik cara analitikal di atas dengan melakukan pengamilan bagi persamaan untuk bentuk arus yang lain.
Kesimpulan
Kesimpulannya, voltan RMS (Root Mean Square) atau voltan Punca Kuasa Dua adalah nilai efektif bagi voltan AC, iaitu nilai yang setara dengan voltan DC yang menghasilkan jumlah tenaga haba yang sama dalam beban resistif. Untuk arus elektrik sinusoid, voltan RMS adalah 0.707 kali voltan puncak. Voltan RMS ini banyak digunakan kerana memudahkan kita untuk mengira kuasa yang dikeluarkan dalam arus ulang alik.
Penukar unit voltan puncak, RMS dan purata
Gunakan alat kalkulator penukar voltan kami untuk memudahkan penukaran unit voltan ke voltan puncak, RMS dan purata di sini:
Kalkulator Penukar Unit Voltan puncak, RMS, dan purata – Pakcik.Engineer